The art of shuffling music
Everyone knows and loves it: The »shuffle« function that is included in every disc- or memory-based music player. If you don’t feel like chosing your »playlist of the day« when you want to listen to your music, you just turn on the shuffle mode and off you go with the finest collection of all tracks on your CD or MiniDisc or hard disk or flash chip. This feature is so popular that a certain computer manufacturer once successfully introduced a MP3 player that was actually based on the shuffle option.
However, there’s something wrong with virtually every shuffle implementation: It’s random.
I can already hear you saying »He gotta be kidding! Randomness is what shuffling is all about!« Well, you’re right. Mostly. The problem with conventional shuffle algorithms is that they are too random. They lack fairness and uniform distribution.
The problem
Imagine that your music collection consists of tracks of three different genres, with a roughly equal number of tracks per genre. For example, you have 10 tracks of genre A, 11 of genre B and 11 of genre C. A truly random shuffle algorithm like it’s employed in almost all player programs and device firmwares would generate shuffle patterns like this one:
AACBBCBACABBCCACCCCABBACBACABABB
This example, short as it is, already exhibits the two main problems of random shuffle algorithms. The first one is the burst of four adjacent C’s in the middle of the sequence, the second one is the lack of B’s in that area (there’s no B for 8 slots, which is quarter of the whole sequence!). Actually, these are two manifestations of the same problem: lack of uniform distribution. A truly random shuffle algorithm of course can, and will, take the liberty of generating such non-uniform spots.
While this behavior is perfectly normal and in fact required e.g. for cryptographic purposes, it’s not very well-suited for shuffling music. Going back to the track/genre metaphor, the »anomaly« in the example would mean that you won’t hear any music of genre B for one quarter of the whole playlist length. Instead, you will hear C-style music over and over again, only interrupted by two brief intermezzos of genre A.
Oh, and before you ask: No, I didn’t make this pattern up. I just let Python’s random.shuffle() run, exactly one time, and this is what I got. If I iterate, I get such a »bad« pattern in about 80% of the cases. Sometimes, there are even two or more areas of non-uniformity. And this is only for 32 tracks – now imagine a real scenario: Even the smallest iPod shuffle model fits 100 tracks, which is already sufficient to make the appearance of boring parts almost certain. Now try to imagine what happens for music collections with track counts in the thousands.
Long story short, if you want shuffled music, you actually don’t want a random playback order. Instead, you want a good, uniformly distributed mix of all the tracks on your disk or flash. How about this:
ABCBCABACBACBCABCACBABCACBACBCAB
This pattern doesn’t have any unusual bursts. Instead it’s nicely aternating between the genres, but without being completely regular. In fact, there’s a simple rule that should be followed to construct good shuffle patterns:
Try to spread the tracks of each logical group as far away from each other as possible.
Unfortunately, this is a lot easier to understand than to implement. I’ll now show one possible approach to turn this maxim into an actual algorithm which I call »Balanced Shuffle«.
The concept
The basic principle of the algorithm is to split the music collection into multiple »logical groups«. The tracks inside each group are then shuffled to obtain a random playback order. If the group is still divisible into sub-groups (say, you grouped into genres, now you sub-group into artists), the Balanced Shuffle algorithm is used for this step. This way, the algorithm is applied recursively until there’s no further classification possible. In this case, the remaining tracks of this (sub-)group are considered equal in style and can thus be shuffled using a conventional method. When the track lists for all groups are collected, the main part of the algorithm (described below) begins: The per-group playlists are merged into a single one, taking care of the »maximum spread« principle.
In practice, there’s still the problem of how to obtain a meaningful classification of the music. Up to this point, I used genres, artists and albums as examples, which could work well if the music is tagged properly. However, this is a bit problematic: Of all criteria, the top-level one – genre – isn’t really reliable. Not only is defining genres a very subjective task, it’s also the sheer mass of available fine-grained genres that poses problems. It might be fine if you specified all the genre tags yourself, constrained to a few basic genres, but it gets worse if you got music from different external sources. Sometimes the genre tag is even missing completely or has a generic value (like »soundtrack«, for example), which would seriously spoil the classification.
That’s why I tend to use another basis for splitting the tracks into groups: The directory structure. Unless you use weird (iTunes-style) music management software, you’re likely to already have a suitable classification in the form of directories and sub-directories, and if you don’t, it’s only a matter of a few minutes to create one. The main benefit is full user control while at the same time not needing specific software for this task. It might seem a bit old-fashioned, and maybe it is, but it’s a simple and flexible solution after all :)
The merge algorithm
The merge algorithm is, in some way, the heart of the whole Balanced Shuffle concept. It takes the already pre-shuffled playlists of each group as input:
Before proceeding with actual merge operation, all the group playlists will be filled up to the length of the longest list (which will therefore remain unchanged). This fill operation doesn’t change the order of the tracks, it just inserts dummy tracks at random intervals, but subject to the »maximum spread« rule:
The merge is then performed by collecting all the tracks column by column, precisely:
- All the tracks of one column are retrieved.
- The dummy tracks are removed.
- The order of the tracks from this column is randomized (using a real random shuffle this time).
- The randomized tracks are appended to the resulting playlist.
- Proceed with the next column.
Here’s one example of how this works:
Here, the tracks from the first column were retrieved. In this case, it was just a track from the red and the blue group, all others were dummies. These two were arranged in a random order, which just so happened to be the reverse order of the originals.
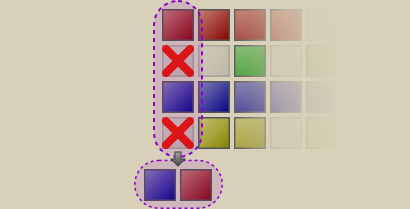
Now, the red, blue and yellow tracks from the second column were re-arranged into the yellow-red-blue order and appended to the already processed track list.
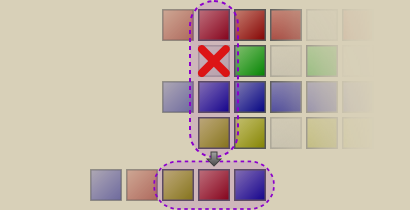
In the third colum, tracks from all groups were present and a yellow-blue-green-red sequence got appended to the track list. This column-for-column approach will now continue until the final Balanced Shuffle playlist (or sub-playlist if we came from a recursive invocation of the algorithm) has been assembled.
One little tweak is made to the shuffle step: If, by accident, the group of the first track of the current column, is the same as the group of the most recently added track of the assembled playlist, it will receive a »penalty« by being moved to the end of the list. For example, if the current playlist is made out of tracks from groups ABCAB and BCA is about to be added, it will be changed into CAB (B moved to the end), yielding ABCABCAB. This technique avoids playing two tracks of the same group consecutively, as long as each column contains more than one non-dummy track. This could be improved by some sort of look-ahead (if the following column has only one track, make sure that the last appended track isn’t from the same group), but in my current implementation, I skipped that part.
The fill algorithm
The only problem left is how to fill the partial track lists up to the required length. As I already wrote, dummy elements need to be inserted at regular yet somewhat random intervals. There are many algorithms that would create a perfectly regular pattern (Bresenham, error diffusion, …) and just as much that would create a perfectly random one (simple random shuffle, random threshold, …). Algorithms that allow for slight randomization are considerably fewer, but still numerous. I tried some of them and finally found one that is sufficiently accurate and still very fast. It has the caveat that it only works reliably if the number of dummy tracks is greater than the number of »real« tracks, but this can be easily bypassed by inverting the problem: Instead of filling up many tracks with few dummies, just fill up few dummies with many tracks.
The basic idea is to split the output list (i.e. the one with the required output length n) into k segments of roughly (but only roughly!) equal length, where k is the number of dummies or the number of tracks, whichever is lower. All these segments will then be filled with one track at the beginning and dummies in the other places – or vice-versa, if there are more tracks than dummies.
The segmentation, in turn, is an iterative process: it computes the lengths of segments one after another. For each segment, the optimal length r is computed first. This is how long the segment would be if the segmentation process was regular; hence, r=n/k. Randomness is acheived by adding noise to r: In my code, I use a +/- 10% deviation from the computed value. r is then converted to an integer value. To avoid overflows due to the randomization, the value is also clipped against both bounds the algorithm requires to work: Every segment needs to be at least 1 element long, but it may not be longer than n–k+1, because k-1 segments must still fit into the sequence after the current one.
After the final value for r is determined, a sequence of this length is added and the values of n and k are updated: k=k-1 (one segment less to go) and n=n–r (the remaining length decreased by the length of the segment).
The result of this procedure is a pattern that’s largely OK, with the exception that it always starts with one of the fewer elements (track or dummy). To fix this, the whole sequence will simply be transposed by a random offset, thus moving the forced element at the beginning to some arbitrary location. Here’s an example of the whole filling process:
????????????????????→ n=20, k=5; r=n/k=4.00, randomized: r=5
X....???????????????→ n=15, k=4; r=n/k=3.75, randomized: r=4
X....X...???????????→ n=11, k=3; r=n/k=3.67, randomized: r=2
X....X...X.?????????→ n=9, k=2; r=n/k=4.50, randomized: r=3
X....X...X.X..??????→ n=6, k=1; r=n=6
X....X...X.X..X.....→ finished, need to add random offset
.X...X.X..X.....X...
Conclusion
As you can see, shuffling music properly isn’t as simple as you might have thought. I just presented one possible algorithm that tries to »do it right«: It produces a random playback order, but at the same time maintains the maximum amount of diversity. I’m not going to say that this is the only method to accomplish this, I’m not even going to say it’s the best one. But it is an approach that works adequately without being too complex. Its Python implementation shuffles my whole iPod nano’s content (almost 700 tracks) in about one second on a modern PC. Actually, shuffling music on iPods is why I wrote the whole thing in the first place: I was not happy with what the built-in »Random Songs« mode offered, so I wanted to improve on that. The result can be seen in CENSORED 0.3.0, which has been released yesterday.

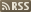 Post Feed
Post Feed

Great post!! :)
Thanks for making it.
interesting…..! to know about the function that i use everyday
This is good, but what method do apple products use?
The_Wizard: Apple has a so-called “smart shuffle” algorithm, but this merely puts higher-rated tracks in front of lower-rated ones. So basically, it’s just random shuffle, followed by a sort-by-rating operation. I don’t know of any product (software or hardware) that uses some kind of smart, balanced or whatever-you-like-to-call-it shuffle based on the principles I described in the text. Well, except CENSORED, of course ;)
Is their anyway that you could create a little ap, that would implament your shuffling skeam, that would create a playlist of the shuffled tracks? I do understand: creating aps take time, and I’d be willing to pay 10-20 bucks for this. I do not own or use an I-Pod at all… Theirfore, I can not try out your already created software. Thanks. Roosterloop.
This post is in refference to the post directly below. You will be wondering: Q: what OS are you using? A: Windows xp Pro. Q: Do you want a command line ap? A: No, just a simple windows app with text please. I am blind, and using a screan Reader, you don’t even need to add any graphics, just a simple: ad directory brows button, a Promo spot directory brows button and output playlist save as dialog box. I would add entire directory of music, or, if it was required by the ap, each genre, one at a time. The output playlist would be ballenced shuffled. Q: Ok, so why now, the, “Promo spot directory brows button”? A: Ok, so basicly what I am wanting to do is use this for a local intranet radio station. I have all the other software, and hardware. This button would pick a random promo spot, in the mp3 format just like all the rest of the tracks, and place it every three tracks. It would be like this three ballenced shuffled tracks, promo spott at random, and back to another three tracks.
I understand this may be a lot to ask, but I am serious about paying you for this app. I think it could be very useful to more people than just myself. Thanks a lot for reading my posts
Roosterloop
Roosterloop: That’s a very interesting proposal, but I doubt that I have time to implement that. What you can do, however, is put up a bid on a site like rentacoder.com. Maybe someone else is able to and willing to help you. Of course, he may use the algorithm presented in this blog post.
I want an mp3 player algorithm that has genre slider bars.
Example:
60’s (Beatles, Doo-Wop, Dean Martin, Neil Diamond, Stones, etc) – 5%
Country (Cash, Willie, Patsy, Hank, etc) – 5%
Punk (Bloodtypes, 48 Thrills, Anxieties, Isotopes, Tranzmitors, etc) – 40%
Autotune Pop (Katie Perry, Pink, Rhianna, Fergie, etc) – 30%
Alt Country (Old 97’s, Whiskeytown, Gerald Collier, etc) – 20%
So instead of saving Playlists, you save Genre Schemes. Workout mode would have me turning up the percentage on Autotune, and down Punk/Alt Country, and off 60’s/Country.
Other people’s genres would OBVIOUSLY differ from mine, But should be useful to may people.
I would say awesome, just what I was looking for
thanks
Well i had a doubt. It you have a playlist which has tracks say:
ABCDE
It you apply shuffle algorithm, whichever even the faulty random.
What is the probability of getting B as second track right after A??
I think it’s 0 as its the nature of the suffling algorithms.
Am i correct? What say?
ADi: Of course it’s not 0. If you randomly shuffle the tracks around, the probability that you get a sequence starting with »AB« is 1/5 * 1/4 = 1/20 = 5%.
Thanks! I needed to sort themed quiz questions and this was very helpful.
There is a programmers discussion of shuffle algorithms here: http://programmers.stackexchange.com/questions/194480/id-like-to-write-an-ultimate-shuffle-algorithm-to-sort-my-mp3-collection
Awesome. The pictures were very helpful. BTW you were mentioned on the Spotify’s blog post and they’ve modified this a bit to use for their shuffling algorithm :D
Wow, helping Spotify to shuffling algorithm, i saw this post very late :) and very late congrats if you still here